Use the Boneh-Durfee attack on low private exponents to recover the original two prime factors comprising the private key and decrypt an encrypted flag.
Challenge Description
Points
175
Solves
47
Description
Decrypt the message!
Solution
First, we untar the contents of the archive:
$ tar xvf bodu_b33593412cf38bc2ebb2eab07c8a14c5.tar.xz
bodu/
bodu/flag.enc
bodu/pub.key
$ cat pub.key
-----BEGIN PUBLIC KEY-----
MIIBHjANBgkqhkiG9w0BAQEFAAOCAQsAMIIBBgKBgAOmFghI+xc0y9D6Is71guhJ
IjrARRDVFQJVa2R20HOX8D3xVSicIBEuh8bzU2HZ62IspKDlLZzYe/cjUmyCa4g4
fQarxCeeNT8SrY7GLqc8RzIaILiWRIiaeSpzFSvHAUuAppPS5YsSP6klw1ax66A3
pNysjY3oCRZ6b8wwxceFAoGAA2WWLo2rp7qS/Ah2il9zs4VPTHmWnVUYoHigNEN8
Rmm9twW+TYuLq/T9oabnFSaeh7KO7LDU4Ccmon+4chhjdAcg9YNojlVn6xBym7DZ
KzItcZlJ5AxXGY12TxxjPl4nfaPTKB7OLOLrTflFvlr8PnhJjtBImyRZBZZk/hXI
ijM=
-----END PUBLIC KEY-----
So, we have some encrypted data and a public key file. Let’s extract some values from that:
$ openssl rsa -noout -text -in pub.key -pubin -modulus
Public-Key: (1018 bit)
Modulus:
03:a6:16:08:48:fb:17:34:cb:d0:fa:22:ce:f5:82:
e8:49:22:3a:c0:45:10:d5:15:02:55:6b:64:76:d0:
73:97:f0:3d:f1:55:28:9c:20:11:2e:87:c6:f3:53:
61:d9:eb:62:2c:a4:a0:e5:2d:9c:d8:7b:f7:23:52:
6c:82:6b:88:38:7d:06:ab:c4:27:9e:35:3f:12:ad:
8e:c6:2e:a7:3c:47:32:1a:20:b8:96:44:88:9a:79:
2a:73:15:2b:c7:01:4b:80:a6:93:d2:e5:8b:12:3f:
a9:25:c3:56:b1:eb:a0:37:a4:dc:ac:8d:8d:e8:09:
16:7a:6f:cc:30:c5:c7:85
Exponent:
03:65:96:2e:8d:ab:a7:ba:92:fc:08:76:8a:5f:73:
b3:85:4f:4c:79:96:9d:55:18:a0:78:a0:34:43:7c:
46:69:bd:b7:05:be:4d:8b:8b:ab:f4:fd:a1:a6:e7:
15:26:9e:87:b2:8e:ec:b0:d4:e0:27:26:a2:7f:b8:
72:18:63:74:07:20:f5:83:68:8e:55:67:eb:10:72:
9b:b0:d9:2b:32:2d:71:99:49:e4:0c:57:19:8d:76:
4f:1c:63:3e:5e:27:7d:a3:d3:28:1e:ce:2c:e2:eb:
4d:f9:45:be:5a:fc:3e:78:49:8e:d0:48:9b:24:59:
05:96:64:fe:15:c8:8a:33
Modulus=3A6160848FB1734CBD0FA22CEF582E849223AC04510D51502556B6476D07397F03DF155289C20112E87C6F35361D9EB622CA4A0E52D9CD87BF723526C826B88387D06ABC4279E353F12AD8EC62EA73C47321A20B89644889A792A73152BC7014B80A693D2E58B123FA925C356B1EBA037A4DCAC8D8DE809167A6FCC30C5C785
Extracting the values:
# the modulus
N = 0x3A6160848FB1734CBD0FA22CEF582E849223AC04510D51502556B6476D07397F03DF155289C20112E87C6F35361D9EB622CA4A0E52D9CD87BF723526C826B88387D06ABC4279E353F12AD8EC62EA73C47321A20B89644889A792A73152BC7014B80A693D2E58B123FA925C356B1EBA037A4DCAC8D8DE809167A6FCC30C5C785
# the public exponent
e = 0x0365962e8daba7ba92fc08768a5f73b3854f4c79969d5518a078a034437c4669bdb705be4d8b8babf4fda1a6e715269e87b28eecb0d4e02726a27fb8721863740720f583688e5567eb10729bb0d92b322d719949e40c57198d764f1c633e5e277da3d3281ece2ce2eb4df945be5afc3e78498ed0489b2459059664fe15c88a33
Interestingly, it has a huge public exponent. However, this isn’t conclusive of anything. So let’s turn to Google with what we can find based on the title of the challenge.
So it looks like we are supposed to read http://crypto.stanford.edu/~dabo/papers/lowRSAexp.ps and perform the attack on the given RSA parameters. However, this cool guy, https://cryptologie.net/article/241/implementation-of-boneh-and-durfee-attack-on-rsas-low-private-exponents/, has written an implementation of the attack in Sage that we can use :D. So plugging in our modulus and public exponent values, we can get our private exponent:
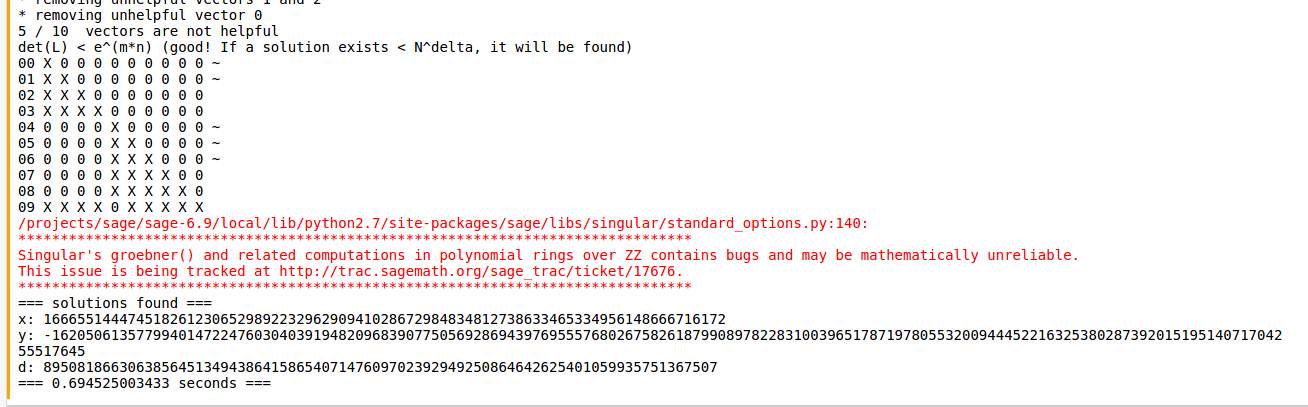
So, having the private exponent, we can recover our original two prime factors. Using this gist, https://gist.github.com/ddddavidee/b34c2b67757a54ce75cb, we can recover our prime factors.
import recover
n = 0x3A6160848FB1734CBD0FA22CEF582E849223AC04510D51502556B6476D07397F03DF155289C20112E87C6F35361D9EB622CA4A0E52D9CD87BF723526C826B88387D06ABC4279E353F12AD8EC62EA73C47321A20B89644889A792A73152BC7014B80A693D2E58B123FA925C356B1EBA037A4DCAC8D8DE809167A6FCC30C5C785
e = 0x0365962e8daba7ba92fc08768a5f73b3854f4c79969d5518a078a034437c4669bdb705be4d8b8babf4fda1a6e715269e87b28eecb0d4e02726a27fb8721863740720f583688e5567eb10729bb0d92b322d719949e40c57198d764f1c633e5e277da3d3281ece2ce2eb4df945be5afc3e78498ed0489b2459059664fe15c88a33
d = 89508186630638564513494386415865407147609702392949250864642625401059935751367507
p, q = recover.RecoverPrimeFactors(n, e, d)
Running the script:
$ python primefactors.py
Found factors p and q
p = 1367950959033448694251101693351971454646908585982174247214456588106744480223502924899594970200721567086593256490339820357729417073968911473368284373028327
q = 1873061312526431600198418914726418187289872964131683141580934527253790685014095254664971230592314176869517383698550622907346640404434127554775124138006963
From here, all we need to do is create our private key and decrypt the file.
import pyasn1_modules.rfc3447
import recover
import gmpy
import pyasn1
import pyasn1.codec.ber.encoder
import base64
def asn1_encode_priv_key(N, e, d, p, q):
key = pyasn1_modules.rfc3447.RSAPrivateKey()
dp = d % (p - 1)
dq = d % (q - 1)
qInv = gmpy.invert(q, p)
#assert (qInv * q) % p == 1
key.setComponentByName('version', 0)
key.setComponentByName('modulus', N)
key.setComponentByName('publicExponent', e)
key.setComponentByName('privateExponent', d)
key.setComponentByName('prime1', p)
key.setComponentByName('prime2', q)
key.setComponentByName('exponent1', dp)
key.setComponentByName('exponent2', dq)
key.setComponentByName('coefficient', qInv)
ber_key = pyasn1.codec.ber.encoder.encode(key)
pem_key = base64.b64encode(ber_key).decode("ascii")
out = ['-----BEGIN RSA PRIVATE KEY-----']
out += [pem_key[i:i + 64] for i in range(0, len(pem_key), 64)]
out.append('-----END RSA PRIVATE KEY-----\n')
out = "\n".join(out)
return out.encode("ascii")
n = 0x3A6160848FB1734CBD0FA22CEF582E849223AC04510D51502556B6476D07397F03DF155289C20112E87C6F35361D9EB622CA4A0E52D9CD87BF723526C826B88387D06ABC4279E353F12AD8EC62EA73C47321A20B89644889A792A73152BC7014B80A693D2E58B123FA925C356B1EBA037A4DCAC8D8DE809167A6FCC30C5C785
e = 0x0365962e8daba7ba92fc08768a5f73b3854f4c79969d5518a078a034437c4669bdb705be4d8b8babf4fda1a6e715269e87b28eecb0d4e02726a27fb8721863740720f583688e5567eb10729bb0d92b322d719949e40c57198d764f1c633e5e277da3d3281ece2ce2eb4df945be5afc3e78498ed0489b2459059664fe15c88a33
d = 89508186630638564513494386415865407147609702392949250864642625401059935751367507
p, q = recover.RecoverPrimeFactors(n, e, d)
print asn1_encode_priv_key(n, e, d, p, q)
Running the script,
$ python gencert.py
Found factors p and q
p = 1367950959033448694251101693351971454646908585982174247214456588106744480223502924899594970200721567086593256490339820357729417073968911473368284373028327
q = 1873061312526431600198418914726418187289872964131683141580934527253790685014095254664971230592314176869517383698550622907346640404434127554775124138006963
-----BEGIN RSA PRIVATE KEY-----
MIICOwIBAAKBgAOmFghI+xc0y9D6Is71guhJIjrARRDVFQJVa2R20HOX8D3xVSic
IBEuh8bzU2HZ62IspKDlLZzYe/cjUmyCa4g4fQarxCeeNT8SrY7GLqc8RzIaILiW
RIiaeSpzFSvHAUuAppPS5YsSP6klw1ax66A3pNysjY3oCRZ6b8wwxceFAoGAA2WW
Lo2rp7qS/Ah2il9zs4VPTHmWnVUYoHigNEN8Rmm9twW+TYuLq/T9oabnFSaeh7KO
7LDU4Ccmon+4chhjdAcg9YNojlVn6xBym7DZKzItcZlJ5AxXGY12TxxjPl4nfaPT
KB7OLOLrTflFvlr8PnhJjtBImyRZBZZk/hXIijMCIgMFAf5Q4Gv9cyFczi132rdn
VnMfqJFtFAclD+MrQCR961MCQBoeZ65rVKhRrAwlNY1/3MNTYmbnvCLq9Hd7boev
r5sSsZe9ylCbaBJpTNAcLQMyYcu4pbZyN9GWL2Y2L+DZjecCQCPDVT5oeWVS4Xqj
YKMCFZJ8oHvcDAaSBogjXyZDah2t1GUXba7y+hzIq012cthpT1VTet6ItF4Ffe+j
y0ZUGbMCIgMFAf5Q4Gv9cyFczi132rdnVnMfqJFtFAclD+MrQCR961MCIgMFAf5Q
4Gv9cyFczi132rdnVnMfqJFtFAclD+MrQCR961MCQAYQGG+1ZJY4Kj345PtCs6DT
J5mRzZxJsQaHV0v7P0gY+mmt/xv/SRrc9KzH5znD68dVY3FWHKqKPWQ+0gdhe6Q=
-----END RSA PRIVATE KEY-----
Decrypting the flag.enc with the private key:
$ openssl rsautl -decrypt -in flag.enc -out plaintext -inkey private.key
$ cat plaintext
ASIS{b472266d4dd916a23a7b0deb5bc5e63f}
Flag: ASIS{b472266d4dd916a23a7b0deb5bc5e63f}

Leave a Comment